Lecture 6

约会博弈

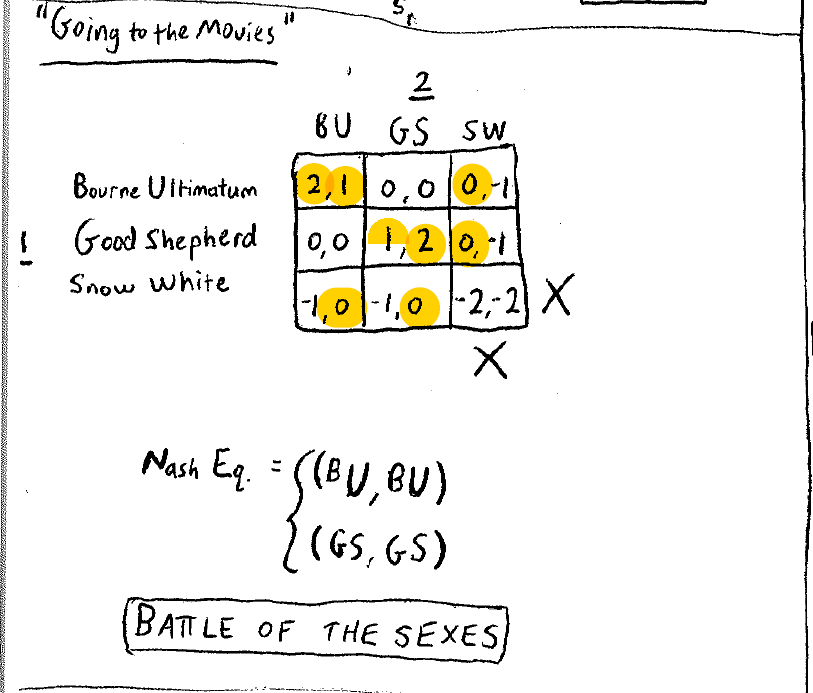
这个纳什均衡的点有一些不同，因为达到纳什均衡时会存在利益的冲突。实际上这种通过沟通达到的纳什均衡是更难的。

Cournot Dupoly 古诺的双寡头模型

玩家：两个公司

策略：生产的产品互为替代品，生产的数量$q_i$。

成本：$c*q$，c是边际成本。

price：$P = a-b*(q_1+q_2)$，生产的数量越多，价格越低。

因此我们可以画出需求曲线：

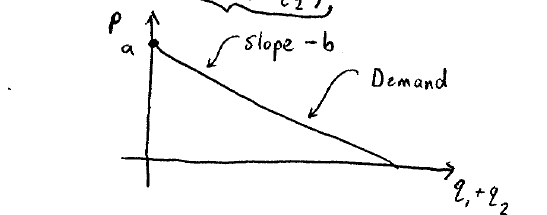
收益：

$u_1(q_1, q_2) = P*q_1-c*q_1$

将$P$代入：$u_1(q_1, q_2) = aq_1-bq_1^2-bq_1q_2-cq_1$

接下来我们求解纳什均衡点。

每一个$q_2$都对应一个$q_1$使得$u_1(q_1, q_2)$最大化，对该式子进行求导：

$a-2bq_1-bq_2-c = 0$

二阶求导：

$-2*b*q_1 < 0$ 因此上面一阶导数是单调递减的，那么最开始的函数是存在最大值，也就是在一阶导数为0的地方。

BR: best response.

那么零点为$BR_1(q_2) = \frac{a-c}{2b} - \frac{q_2}{2}$

同理可以得到玩家2的最佳对策：$BR_2(q_1) = \frac{a-c}{2b} - \frac{q_1}{2}$

这两条最佳对策的曲线的交点就是纳什均衡点。

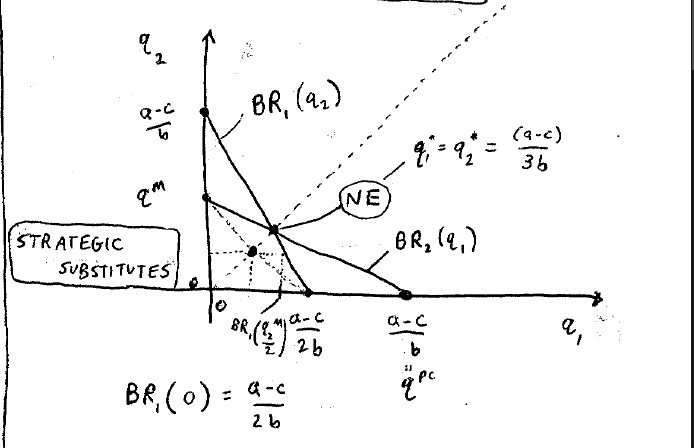
这张图里面有非常多的有趣的信息：

当玩家2生产数量$q_2=0$时，此刻玩家1形成垄断，那么垄断时生产的数量应该是多少？

应该是边际利润等于边际成本的时候，此刻为垄断生产的数量。

此刻我们需要补充一些经济学的知识：

$P = a-bq_1\\ 总收益为TR = P*Q = a*q_1-b*q_1^2\\ 边际收益MR是TR关于Q的导数。\\（这句其实很好理解，我们对总利润和总数量进行微小的变化，两者的比率自然是边际利润） 所以MR = a-2*b*q_1\\ 如下图中红线所示$

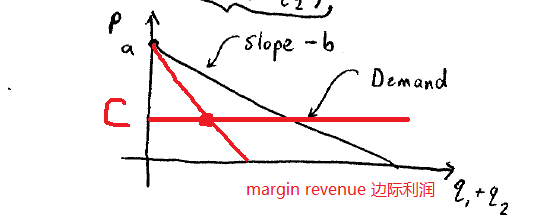
也就是

$a-2b*(q_1) = c$

求得$q_1 = \frac{a-c}{2b}$，这就是垄断生产的产量。与上面的最佳对策算出来的结果是一致的。

当$q_2$为多少的时候，使得$q_1$停产？

当边际利润与需求曲线的交点就是。也就是这个时候的生产成本等于卖出的价格的时候，这个时候企业一毛钱都挣不到。

$q_2 = \frac{a-c}{b}$，专业名词：完全竞争产出。

总结

这个和合伙人的博弈不同，合伙人是其中一个玩家约投入，那么该玩家也会越投入；而这个游戏是相反的（也就是曲线的斜率是负的）。

什么时候行业利润最大？垄断的时候。

但是还有一种方法：那就是两家签订协议，大家都生产垄断的数量的一半（1. 这样是违法的；2. 同时虽然表面签订了协议，但是因为不是最佳对策，因此可能会偷偷增加生产，最终达到纳什均衡；3. 实际上还会有更多的公司加入到其中）。

将完全竞争、达到纳什均衡、垄断的数量和价格进行对比：